mitzVah - the "worst" pangrams part 2
update apr 2: I accidentally deleted this article and now have re-posted it
in part 1, I introduced the spelling bee and the concept of the "worst" pangram, which I defined as the one which produced the fewest possible words. Then I wrote and described a program that found them, and labelled equivoke the Worst Pangram™.
I thought I was done getting nerdsniped after that, but a few people helpfully provided bits of information I was missing the first time, and I also thought a bit more about the problem to change its definition a bit.
more better information
People shared two bits of information with me that I didn't have when I started:
- On mastodon, Brad Greenlee shared a wordlist he's been working on for his spelling bee solver. This pared-down scrabble wordlist is much closer to what a real spelling bee word list looks like
- On reddit,
cearrachinformed me that a Genius score is 70% of the total points for a puzzle.
I took Brad's word list (thanks!) and added calculation of the word score and each pangram's total score. I didn't mention how words are scored in the first article:
- a 4 letter word is worth 1 point
- any word with more than 4 letters is worth as many points as it has letters
- a pangram scores a 7 point bonus
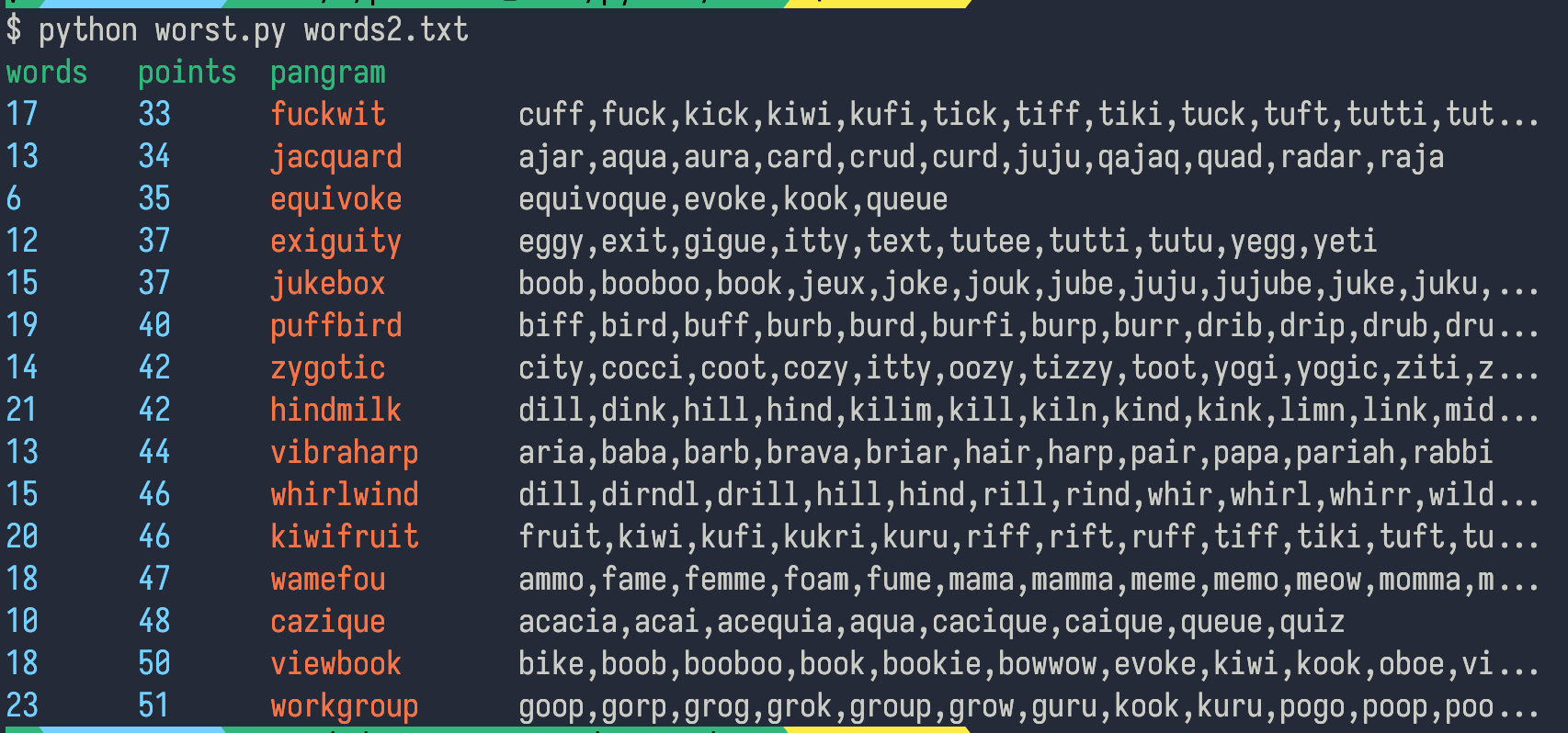
This led to a funny result, where fuckwit was the new "worst" pangram:
back to the beginning
The initial prompt for this exploration was a question about whether there were any spelling bee puzzles where just the pangram would get you to the "genius" level.
I had changed the question to suit the knowledge I had at the start, but now I realized I had enough information to try and answer the original question.
I looked at that list and realized that if you set the puzzle as jacquard, and used the q as a required letter, you'd have only the pangram and three additional words: aqua, qajaq (an alternative spelling of kayak, apparently!) and quad. That would give you:
jacquard: 7 + 8 = 15 pointsaqua: 1qajaq: 5quad: 1
So jacQuard would result in a puzzle where the pangram was responsible for 15/22 points, or just a tiny hair below genius level. Could we do better?
I took the same program I used in part 1 and added a search through each letter of the pangram, scoring the result of making that letter required.
Here's a table of every pangram my program finds that would reach genius level all by itself:
| score | pangram | words |
|---|---|---|
| 14 | mitzvah | |
| 14 | princox | |
| 15 | vagotomy | |
| 15 | viburnum | |
| 15 | conflux | flux |
| 15 | jukebox | jeux |
| 15 | cazique | quiz |
| 15 | gazpacho | |
| 16 | bovinity | viny |
| 16 | checkbox | exec |
| 16 | foxhound | doxx |
| 16 | quixote | exit,text |
| 17 | bikeway | bike,kiwi,wiki |
| 17 | judicial | jail,juju |
| 17 | exiguity | exit,text |
| 17 | tubifex | exit,ibex,text |
| 17 | activize | zeta,ziti |
| 18 | jacquard | card,crud,curd |
| 18 | highjack | gaga,high,jagg |
| 18 | bullwhip | whip,whup,will |
| 18 | oxazepam | apex,exam,expo |
| 19 | gazpacho | agog,gaga,goop,pogo |
| 19 | puffbird | burp,drip,puff,purr |
| 19 | exiguity | eggy,itty,yegg,yeti |
| 19 | buzzword | bozo,buzz,orzo,ouzo |
| 19 | zucchetto | chez,ooze,ouzo |
| 20 | mitzvoth | vomit |
| 20 | vanguard | guava |
| 20 | duckwalk | claw,wack,walk,wall,waul |
| 20 | kiwifruit | kiwi,twit,wiki,writ |
| 20 | quixotic | toxic |
| 21 | bijective | beet,bite,jibb,jibe,vibe |
| 21 | cheapjack | hajj,jack,jake,jape,jeep |
| 21 | equivoke | evoke,kook |
| 21 | jacquard | aqua,aura,crud,curd,juju,quad |
| 21 | vibraharp | brava |
| 21 | boxthorn | hotbox |
| 21 | pyxidium | mixup,pixy |
| 22 | tubificid | biff,buff,cuff,duff,tiff,tuft |
| 22 | exemptive | peeve,veep |
| 22 | ivorybill | ivory,viol |
| 22 | phototoxic | toxic |
| 23 | toxicologic | toxic |
| 24 | epexegetic | epigeic |
| 25 | aquacultural | aqua,quart |
implementation
Following the same start of the program I used to find the word count for every pangram in part 1, I added a couple more loops:
- let $scoresWithReqLetters$ be a list of tuples ($totalScore$, $requiredLetter$, $pangram$)
- For each pangram
- find all words that match the pangram
- for each letter in the pangram
- sum the score of each word that contains the letter
- add that score, the letter, and the pangram to $scoresWithReqLetters$
- Sort $scoresWithReqLetters$
- For each pangram
- if the score of the pangram is > 70% of $totalScore$, print it out
The implementation in python:
@cache
def wscore(w):
return (1 if len(w) == 4 else len(w)) + (7 if len(allwordsets[w]) == 7 else 0)
# find all matches for each pangram, then the score for each possible required
# letter
scores_with_req_letters = []
pangram_matches = {}
for points, _, pangram in pangrams:
ps = allwordsets[pangram]
matches = [w for w in allwords if allwordsets[w].issubset(ps) and w != pangram]
for l in ps:
lmatches = [m for m in matches if l in m]
pangram_matches[(pangram, l)] = lmatches
score = len(pangram) + 7 + sum(wscore(m) for m in lmatches)
scores_with_req_letters.append((score, l, pangram))
@cache
def hl(w: str, l: str) -> str:
return f"{red}{w.replace(l, f'{yellow}{l}{red}')}"
red = "\N{esc}[0;31m"
green = "\N{esc}[0;32m"
yellow = "\N{esc}[0;33m"
blue = "\N{esc}[0;34m"
reset = "\N{esc}[0m"
print(f"{green}points\tpangram\t\twords")
scores_with_req_letters.sort()
for points, l, pangram in scores_with_req_letters:
matches = pangram_matches[(pangram, l)]
panscore = wscore(pangram)
total = panscore + sum(wscore(m) for m in matches)
if (panscore / total) > 0.7:
matchstr = ",".join(matches)
if len(matchstr) > 60:
matchstr = matchstr[:59] + "..."
print(
f"{blue}{points: <8}{hl(pangram, l)}{' ' * (16-len(pangram))}{reset}{matchstr}"
)
I didn't dive much into performance, but here's a few notes:
- pypy runs this program quite a bit faster than cpython on my machine, roughly 46s to 77s
- The program spends almost all its time finding every matching word for every pangram, if I were to speed it up that would be the loop I would target
- Caching the construction of all sets at the beginning of the run was a simple and significant performance win
With that, I feel like I can finally wash my hands of this problem! (Maybe? we'll see!)