What are the "worst" spelling bee pangrams?

Thomas Ptacek wondered on mastodon whether there were any Spelling Bee pangrams that would get you to the highest scoring level on spelling bee just by finding that word.

I like to play spelling bee, and this seemed like a solvable problem, so I took a hack at it.

(update: there's a part 2)

The setup

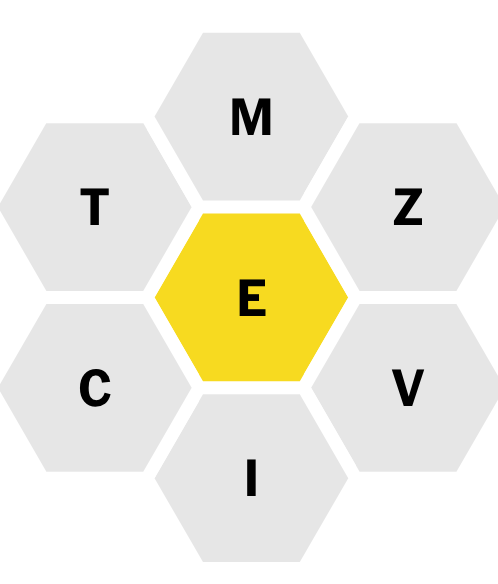
In the spelling bee, you're given 7 letters, one of which must be in every word, and asked to make as many words as possible out of those seven.

If you use all seven letters, that's called a $pangram$. Every day's puzzle is guaranteed to have at least one pangram.

Unfortunately, there were a couple of things I didn't know:

• A complete list of valid spelling bee words
• The amount of points you need to score to reach the "genius" level

So I decided to use a scrabble wordlist I found online, and to instead just find the "worst" pangrams, the ones somebody could make the fewest words out of.

The search

The basic algorithm I settled on was:

• step 1 calculate the score of every set of seven letters
• let $scores$ be a hash of ${set(letters): int(score)}$ which defaults to 0 and represents the number of words playable via the given set of seven letters
• For every word in the word list
  • make a set $s$ of unique letters in the word
    • add that set to every set of seven letters of which it's a subset
    • for every combination $c$ of $7-length(s)$ letters not in that set:
      • add one to $scores[c]$
• step 2 Now $scores$ has the score of every set of 7 letters that can be reached from the given word list, so we can iterate through each $pangram$, find its score, and sort the list to find the worst.
• let $pangrams$ be a list of tuples $(n_{words}, pangram)$
• For each word in the word list
  • make a set $s$ of unique letters in the word
  • if there are seven letters, it's a pangram. Look up its score in $scores$ and add it to $pangrams$
• Sort the $pangrams$ list
• step 3 Print out the results

The final code looks like this:

# worst.py: print the worst possible pangrams for the New York Times spelling bee

from collections import Counter
from itertools import combinations

# the spelling bee never includes the letter "s"
alphabet = frozenset("abcdefghijklmnopqrtuvwxyz")
allwords = set(line.strip() for line in open("words.txt") if "s" not in line)

# get the score of every seven-letter combination
score = Counter()
for word in allwords:
    ws = frozenset(word)
    if 3 < len(word) and len(ws) < 7:
        for letters in combinations(alphabet - ws, 7 - len(ws)):
            score[ws.union(letters)] += 1

# get a list of pangrams and sort it
pangrams = [
    (score[frozenset(word)] + 1, word)
    for word in [line.strip() for line in open("words.txt")]
    if "s" not in word and len(set(word)) == 7
]
pangrams.sort()

# format the results
red = "\N{ESC}[0;31m"
green = "\N{ESC}[0;32m"
blue = "\N{ESC}[0;34m"
reset = "\N{ESC}[0m"
print(f"{green}words\tpangram")
for n, pangram in pangrams[:15]:
    ps = set(pangram)
    matches = ",".join(
        [
            w
            for w in [l.strip() for l in open("words.txt")]
            if set(w).issubset(ps) and len(w) > 3 and w != pangram
        ]
    )
    if len(matches) > 60:
        matches = matches[:59] + "..."
    print(f"{blue}{n: <8}{red}{pangram: <15}{reset}{matches}")

It's not efficient code, but it runs fast enough that I didn't worry about making it any faster.

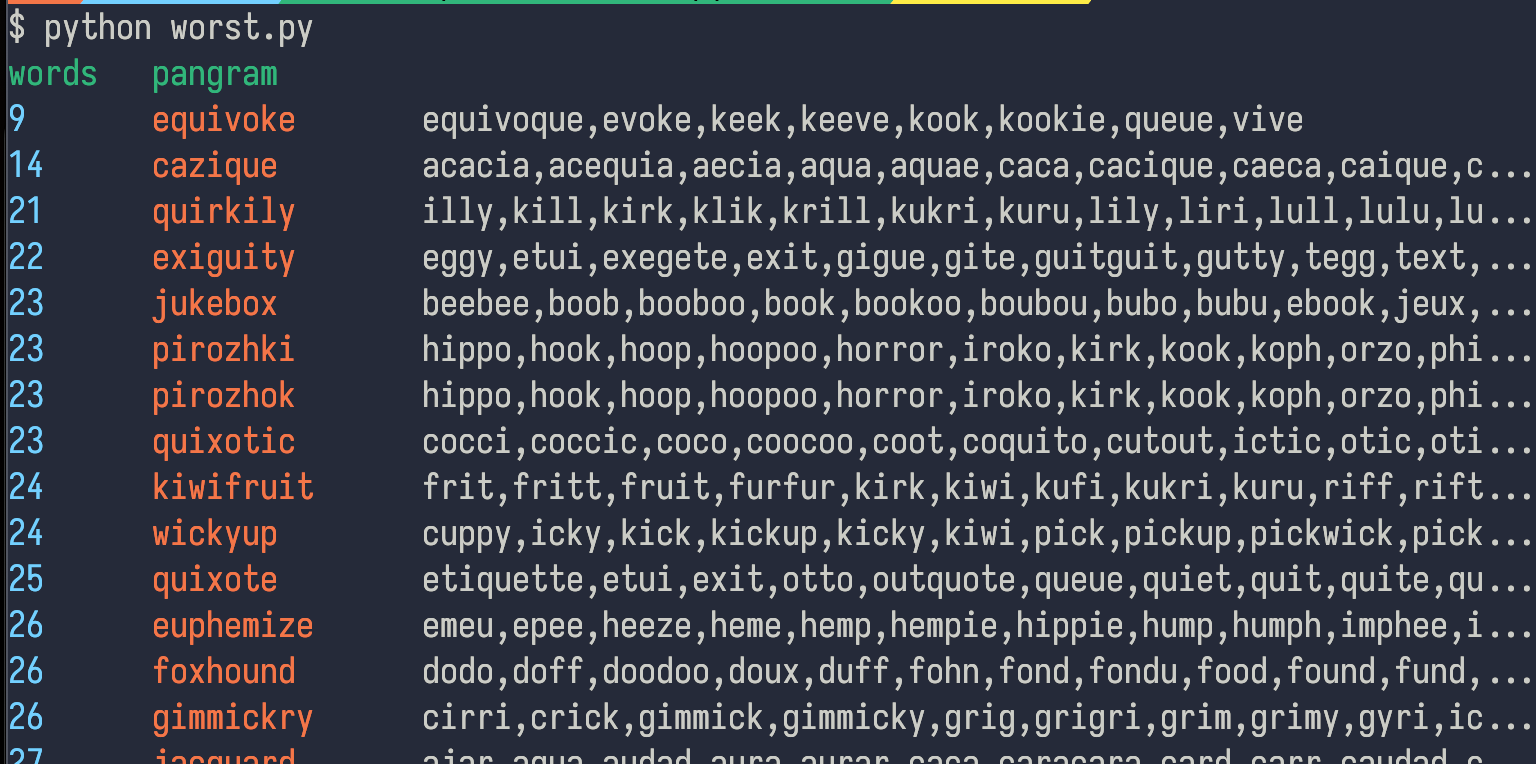
The output of the program is:

So according to it, equivoke is the "worst" possible pangram.

For kicks, I looked up some of the words on sbsolver. According to that site equivoke has a mere 6 legal words in the spelling bee dictionary: equivoque, evoke, kook, queue, and quooke.